Exercices
révision 1.0 (16/6/2013)
Exercice 1
Énoncé
Soit le système matériel plan, constitué d’une poutre droite soumise à 1 force verticale « P » et un force horizontale « Q ».
- Déterminer les réactions d’appuis ;
- Établir les équations représentant les variations de N, Ty, Mtz ;
- Représenter ces variations sur un graphique.
Pour résoudre ces types de problèmes il faut suivre la méthodologie suivante:
1/ Choisir un repère (voir chapitre N°1) ;
2/ Identifier les inconnues aux réactions d’appuis (voir chapitre N°1) ;
3/ Ecrire et résoudre les 3 équations fondamentale de la statique ;
4/ Découper la poutre en autant de « sections droites » que « d’évènements » ;
Un événement est constitué par une action, une réaction ou un changement de direction de la poutre. Il faut « lire « la structure de gauche à droite en identifiant chaque évènement. Dans notre exemple il existe donc 2 sections à étudier. Les positions de ces sections sont définies depuis l’origine du repère choisi.
5/ Exprimer dans chaque section les valeurs de N, Ty, Mtz ;
6/ Représenter graphiquement les variations.
Résolution
1/ Choix du repère (voir sur la figure)
2/ Identifications des inconnues d’appuis :
- Un appuis simple en A = Va inconnue
- Une articulation en B = Vb et Hb inconnues
- Ces inconnues sont prises, par hypothèse positive selon xAy
3/ Equations fondamentales de la statique
Cette équation (1) permet immédiatement de déterminer Hb!
Cette 2eme équation comprend 2 inconnues, elle ne peut être résolue
Cette 3eme équation permet d’extraire Vb:
A partir de l’équation N° (1) nous pouvons exprimer Va :
4/ Déterminer N, Ty, Mtz
La poutre doit être étudiée en 2 « tronçons ». En parcourant la poutre de gauche à droite depuis le point »A », nous rencontrons les « événements » suivants:
1/ Présence de la réaction d’appuis « Va » et de la force horizontale »Q »
2/ Présence de la force « P »
Il faut donc créer 2 sections, que nous appellerons S1 et S2 d’abscisse « x ».
Etude de N, Ty, Mtz dans « S1 » 0<x<a
N+ Q = 0
Ty+Va = 0
Mtz-Va.x= 0
équation d’une droite, pour x=0 Mtz =0; pour x=a Mtz = -a.Va
Etude de N, Ty, Mtz dans « S2 » a<x< (a+b)
N+Q = 0
Ty+Va-P = 0
Mtz-Va.x+P(x-a) = 0
équation d’une droite Mtz=aVa pour x=a et Mtz=0 pour x=o
5/ Représentation graphique de N, Ty, Mtz
Exercice 2
Énoncé
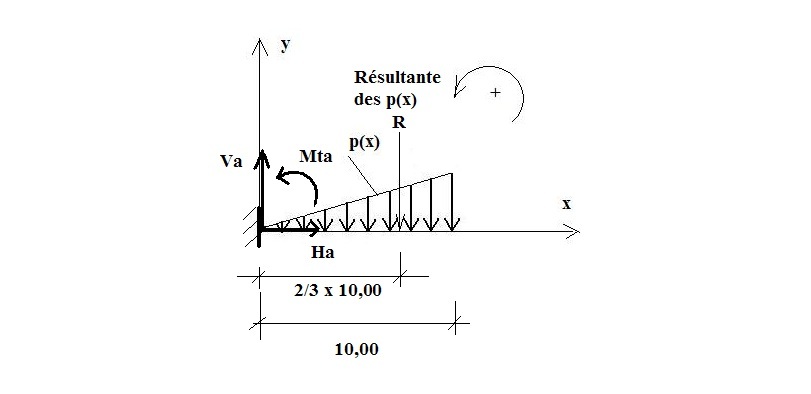
Soit une poutre droite AB, à plan moyen, chargée par une charge répartie uniformément de valeur « p » par ml.
Déterminer les variations de N, Ty, Mtz
Résolution
1/ Choix du repère (voir sur la figure)
2/ Identifications des inconnues d’appuis :
Un appuis simple en A = Va inconnue
Un appui en B = Vb inconnue
Ces inconnues sont prises, par hypothèse positive selon xAy
3/ Equations fondamentales de la statique
Il n’existe aucune force ni réaction horizontale, l’équation est donc vérifiée.
Cette 2eme équation comprend 2 inconnues, elle ne peut être résolue
Cette 3eme équation permet d’extraire Vb :
A partir de l’équation N° (1) nous pouvons exprimer Va:
4/ Déterminer N, Ty, Mtz
La poutre doit être étudiée en 1 « tronçon ». En parcourant la poutre de gauche à droite depuis le point »A », nous rencontrons les « évènements » suivants:
1/ Présence de la réaction d’appuis « Va » et de la force répartie « p ».
Il faut donc créer 1 section, que nous appellerons S d’abscisse « x ».
Etude de N, Ty, Mtz dans « S » 0<x<L
Cette équation, du 2eme degré, représente une parabole
5/Représentation graphique de N, Ty, Mtz
Exercice 3 (TD)
Etudier les variations de N, Ty Mtz : F1 = 3800 N ; F2=5050 N; F3 = 2200 N
Exercice 4 (TD)
Étudier la variation de N, Ty et Mtz le long de cette structure plane, chargée uniquement dans son plan.
Exercice 5 (TD)
Etudier les variations de N Ty Mtz de cette poutre droite chargée dans son plan.
Exercice 6 (TD)
Etudier les variations de N, Ty, Mtz dans cette poutre droite chargée dans son plan.
Exercice 7 (TD) Problème de statique
La figure suivante représente un portique typique en acier (charpente ou autre) de façon schématique :
Calcul des réactions d’appuis (forces externes)
On applique le principe de la statique somme des forces = 0 :
Le système se compose ici de deux barres de longueurs respectives S1 et S2 et d’inertie Iz1 et Iz2.
Les appuis externes sont articulés en A et en C et le système est soumis à une force P. (voir figure ci-dessous)
Calcul de N, T et Mz (forces internes)
Pour la détermination du moment fléchissant , les éléments suivants sont à considérer :
Le moment fléchissant est nul aux appuis A et C.
Le moment est positif et passe par un maximum le long de la travée AB.
Le moment s’inverse et il repasse par une valeur en C avant de baisser sur la travée BC jusqu’à M=0 en C.
Si l’on isole la travée CB on représente les efforts internes comme ci-dessous. On remarque que le sens de l’effort tranchant et le celui moment ont changés de sens par rapport à la situation typique :